Graph Edges Classification

While using depth first search to explore a graph, the DFS can be modified to find the different edges in the DFS tree formed.

Let us go through each component one by one and try to understand it all.

/* 	Function to perform DFS traversal on a graph
*	u:	source vertex
*	visited:boolean vector to mark vertices as visited
*	adj[]:	array of vectors to store graph as adjacency list
*/
void dfs(int u, vector <bool> &visited, vector <int> adj[]) {
	visited[u] = true;
	for (auto v: adj[u]) {
		if (!visited[v]) {
			dfs(v, visited, adj);
		}
	}
}

This above simple DFS function visits all the vertices in the graph reachable from the source vertex.

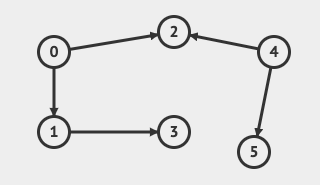Consider the graph on the left, a call on DFS with source as 0 would mark vertices 1, 2, and 3 as visited. Now, calling DFS with source as 4 would not visit the edge $4 \rightarrow 2$

So, which edges are exactly traversed during DFS?

Precisely, an edge $u \rightarrow v$ is visited only when vertex $v$ is marked as unvisited. Thus, these edges form a tree, called the depth-first-tree of the graph starting at the source.
If the graph is disconnected, what we get will be called a DFS forest.
The edges in a DFS-Tree are what are called as the tree edges in the original graph.
The edges $0 \rightarrow 1$, $0 \rightarrow 2$, $1 \rightarrow 3$ are few tree edges.

What is the edge $4 \rightarrow 2$ known as, then?

It is called as a cross-edge since it connects two different DFS trees in the DFS forest. What if we got only one DFS tree? Can it have cross edges? Yes, it would then connect two different subtrees.

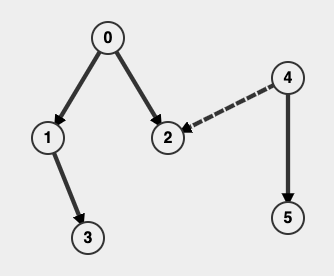This is the DFS forst for the above graph.

There are also two other types of edges known as -

• Back edge
• Forward edge